How to calculate percentiles? Formula and procedure

Let's see what it is and how we can calculate percentiles in a research context.

Nowadays it is common that we have to work with large amounts of data, regardless of whether we are engaged in research or other sectors.

For this we need to be able to operate with them, and often compare and sort data with each other. And in this sense, it can be useful to use position measures through which to separate the total values of that measured in several parts in order to locate in which position one of them is. One of the best known and most useful is the percentile. But... what is a percentile? How to calculate percentiles? Let's see it throughout this article.

What is a percentile?

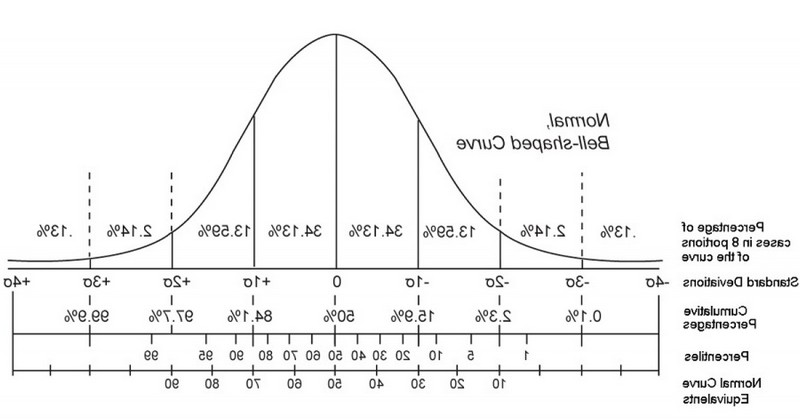
One of the most common measures of data position is known as percentile or centile, which involves dividing the total of what is being measured into 99 parts to obtain a total of 100 equal parts. involves dividing the total of what is being measured into 99 parts to obtain a total of 100 equal parts.. Thus, the whole of what is being measured is represented somewhere in these 99 parts, and the particular data will occupy a position among these parts. This is a type of quantile or fractile, values that allow data to be separated into groups with the same number of values.

In other words, the percentiles are each of the positions occupied by some data when the totality of the existing data is divided into one hundred parts, marking the position that leaves below itself a certain percentage of the population corresponding to the value of the percentile per se (i.e. for example the percentile 1 is the one that leaves below 1%). It also leaves behind another relevant percentage.

Related concepts

The concept of percentile is intimately linked to that of percentage, but nevertheless they are different conceptsWhile the percentage is a mathematical calculation that allows us to visualize a given quantity as a fraction between one hundred equal parts, the percentile indicates the position that a data must occupy to be below the corresponding percentage.

Likewise, the percentile is a value that is also associated with other measures of position. is also associated with other measures of position, such as quartiles or deciles.. The difference lies in the number of divisions and the scale on which we observe the position of our data. In fact, quartiles and deciles correspond to different percentiles, since they are simply the position of data on different scales. The different quartiles correspond to the 25th, 50th and 75th percentiles, while the deciles correspond to the 10th, 20th, 30th, 40th, 40th, 50th, 50th, 60th, 70th and 90th percentiles.

What are they for?

Knowing what a percentile is and how to calculate it, although it may not seem so, can be very useful in many areas. The percentile is nothing more than a value that allows us to make comparisons and allows us to make comparisons and rankings between subjects, cases or the degree of existence of a factor or variable in a set, something that allows us to work at a lower level.This allows us to work at a very easily understandable level with more or less extensive data sets and to establish a position for those we are obtaining.

This, at a practical level, can help us to determine, for example, whether an attribute or variable is within normal values or whether it is below or above the mean. Examples of this are that they are helpful in determining whether a neuropsychological function is altered or not, whether intelligence levels are within the normal range if we compare the results of a subject with those of its reference population or if a child has a weight and height close to or far from the average for his age.

Calculating percentiles: how to do it?

Calculating percentiles is a relatively simple process, it is enough to have all the data represented in the same way and perform a simple calculation. However, this requires not only to have a specific data, but also to be clear about what type of score is to be ordered and with respect to what and with whom the comparison is to be made.

In fact, if we use different evaluation instruments, we will often see that there are reference tables to assess between which values a given percentile oscillates in order to be able to associate the data obtained experimentally with that percentile. These are carried out with exhaustive measurements with a representative sample of the reference population. of the reference population.

When we have to calculate a percentile it is necessary to take into account first of all whether we are working with ordered or unordered data. When the data are not grouped or ordered, the position in which the percentile is found can be calculated by dividing the product of the percentile by the number of elements of the sample from which we start by one hundred. The formula would be P=(k*n)/100.

When we are dealing with an ordered data set, we can follow the formula Px=Lri+((kn/100 - Fa)/f)(Ac). Thus, it will suffice to add the lower limit of the class where the percentile is to the product between the amplitude of the class and the quotient between the subtraction of the position minus the previous accumulated frequency and the total frequency.

Likewise, finding a given percentile of a data set (e.g. finding the 25th percentile of a data set or database) only requires dividing the number of values smaller than the one we have by the total number of values and multiplying this result by one hundred.